Background
Start by setting a few parameters; this is the base set of parameters we’ll use.
library(plant)
library(parallel)
n_cores = max(1, detectCores() - 1)
params <- scm_base_parameters("FF16")
params$control$equilibrium_solver_name <- "hybrid"Fitness landscape
First, compute the space that any strategy can exist along the leaf mass area (LMA) axis:
bounds <- viable_fitness(bounds_infinite("lma"), params)
bounds## lower upper
## lma 0.02533822 4.989169Generate a set of trait values across this range and compute the fitness landscape:
lma <- trait_matrix(seq_log_range(bounds, 101), "lma")
fitness <- fitness_landscape(lma, params)
plot(lma, fitness, type="l", log="x", las=1, ylab="Fitness (empty environment)")
abline(h=0, col="grey")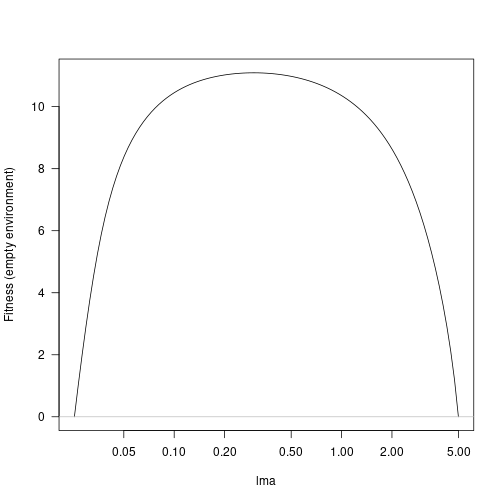
Simulating arrivals
Any trait value along this point can persist, so start with random sample:
lma_sample <- c(0.062, 0.117, 0.970, 2.79)This function takes an LMA value, introduces it to the community, runs that out to equilibrium seed rain. If run interactively it will produce a lot of output:
add_eq <- function(x, p) {
p <- expand_parameters(trait_matrix(x, "lma"), p, mutant=FALSE)
equilibrium_seed_rain(p)
}
patches_eq <- mclapply(lma_sample, add_eq, params, mc.cores = n_cores)Then compute fitness landscapes for each of these:
fitness_sample <- mclapply(patches_eq,
function(p, lma) fitness_landscape(lma, p),
lma, mc.cores = n_cores)
fitness_sample <- do.call("cbind", fitness_sample)
matplot(lma, fitness_sample, lty=1, type="l",
log="x", ylim=c(-5, max(fitness_sample)))
abline(h=0, col="grey")
points(lma_sample, rep(0, 4), col=1:4, pch=19)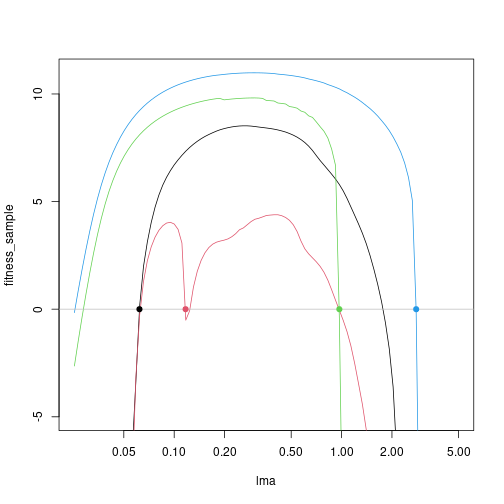
For this system, there is an evolutionary attractor around LMA values of 0.0825:
lma_attr <- 0.0825
patch_eq_attr <- add_eq(lma_attr, params)## [2021-02-25 12:22:37.182] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:22:37.182] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:22:39.387] schedule> 1: Splitting {20} times (141)
## [2021-02-25 12:22:39.387] schedule> 1: Splitting {20} times (141)
## [2021-02-25 12:22:41.755] schedule> 2: Splitting {9} times (161)
## [2021-02-25 12:22:41.755] schedule> 2: Splitting {9} times (161)
## [2021-02-25 12:22:44.277] equilibrium> eq> 1: {1} -> {19.97185} (delta = {18.97185})
## [2021-02-25 12:22:44.277] equilibrium> eq> 1: {1} -> {19.97185} (delta = {18.97185})
## [2021-02-25 12:22:48.013] schedule> 1: Splitting {34} times (141)
## [2021-02-25 12:22:48.013] schedule> 1: Splitting {34} times (141)
## [2021-02-25 12:22:52.780] schedule> 2: Splitting {27} times (175)
## [2021-02-25 12:22:52.780] schedule> 2: Splitting {27} times (175)
## [2021-02-25 12:22:58.469] schedule> 3: Splitting {9} times (202)
## [2021-02-25 12:22:58.469] schedule> 3: Splitting {9} times (202)
## [2021-02-25 12:23:04.018] schedule> 4: Splitting {1} times (211)
## [2021-02-25 12:23:04.018] schedule> 4: Splitting {1} times (211)
## [2021-02-25 12:23:09.563] equilibrium> eq> 2: {19.97185} -> {17.15125} (delta = {-2.820598})
## [2021-02-25 12:23:09.563] equilibrium> eq> 2: {19.97185} -> {17.15125} (delta = {-2.820598})
## [2021-02-25 12:23:15.811] schedule> 1: Splitting {1} times (212)
## [2021-02-25 12:23:15.811] schedule> 1: Splitting {1} times (212)
## [2021-02-25 12:23:22.050] equilibrium> eq> 3: {17.15125} -> {17.31508} (delta = {0.1638286})
## [2021-02-25 12:23:22.050] equilibrium> eq> 3: {17.15125} -> {17.31508} (delta = {0.1638286})
## [2021-02-25 12:23:28.317] equilibrium> eq> 4: {17.31508} -> {17.30373} (delta = {-0.01134973})
## [2021-02-25 12:23:28.317] equilibrium> eq> 4: {17.31508} -> {17.30373} (delta = {-0.01134973})
## [2021-02-25 12:23:28.317] equilibrium> Reached target accuracy (delta 1.13497e-02, 6.55482e-04 < 1.00000e-03 eps)
## [2021-02-25 12:23:28.317] equilibrium> Reached target accuracy (delta 1.13497e-02, 6.55482e-04 < 1.00000e-03 eps)
## [2021-02-25 12:23:28.318] equilibrium> Iteration 1 converged
## [2021-02-25 12:23:28.318] equilibrium> Iteration 1 converged
## [2021-02-25 12:23:28.318] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:23:28.318] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:23:32.107] schedule> 1: Splitting {38} times (141)
## [2021-02-25 12:23:32.107] schedule> 1: Splitting {38} times (141)
## [2021-02-25 12:23:37.236] schedule> 2: Splitting {22} times (179)
## [2021-02-25 12:23:37.236] schedule> 2: Splitting {22} times (179)
## [2021-02-25 12:23:42.919] schedule> 3: Splitting {11} times (201)
## [2021-02-25 12:23:42.919] schedule> 3: Splitting {11} times (201)
## [2021-02-25 12:23:49.171] schedule> 4: Splitting {1} times (212)
## [2021-02-25 12:23:49.171] schedule> 4: Splitting {1} times (212)
## [2021-02-25 12:23:55.448] equilibrium> eq> 1: {17.31508} -> {17.30575} (delta = {-0.009332469})
## [2021-02-25 12:23:55.448] equilibrium> eq> 1: {17.31508} -> {17.30575} (delta = {-0.009332469})
## [2021-02-25 12:23:55.449] equilibrium> Keeping species
## [2021-02-25 12:23:55.449] equilibrium> Keeping species
## [2021-02-25 12:24:01.719] equilibrium> eq> 2: {17.31508} -> {17.30575} (delta = {-0.00933248})
## [2021-02-25 12:24:01.719] equilibrium> eq> 2: {17.31508} -> {17.30575} (delta = {-0.00933248})
## [2021-02-25 12:24:07.997] equilibrium> eq> 3: {17.31508} -> {17.30575} (delta = {-0.00933248})
## [2021-02-25 12:24:07.997] equilibrium> eq> 3: {17.31508} -> {17.30575} (delta = {-0.00933248})
## [2021-02-25 12:24:14.301] equilibrium> eq> 4: {17.31508} -> {17.30575} (delta = {-0.009333543})
## [2021-02-25 12:24:14.301] equilibrium> eq> 4: {17.31508} -> {17.30575} (delta = {-0.009333543})
## [2021-02-25 12:24:20.375] equilibrium> eq> 5: {17.30636} -> {17.30628} (delta = {-8.162057e-05})
## [2021-02-25 12:24:20.375] equilibrium> eq> 5: {17.30636} -> {17.30628} (delta = {-8.162057e-05})
## [2021-02-25 12:24:20.375] equilibrium> Solve 1 converged
## [2021-02-25 12:24:20.375] equilibrium> Solve 1 converged
## [2021-02-25 12:24:20.376] equilibrium> Accepting solution via solver
## [2021-02-25 12:24:20.376] equilibrium> Accepting solution via solver
fitness_attr <- fitness_landscape(lma, patch_eq_attr)
plot(lma, fitness_attr, log="x", type="l", las=1,
xlab="Leaf mass per unit leaf area", ylab="Fitness")
abline(h=0, col="grey")
points(lma_attr, 0, pch=19)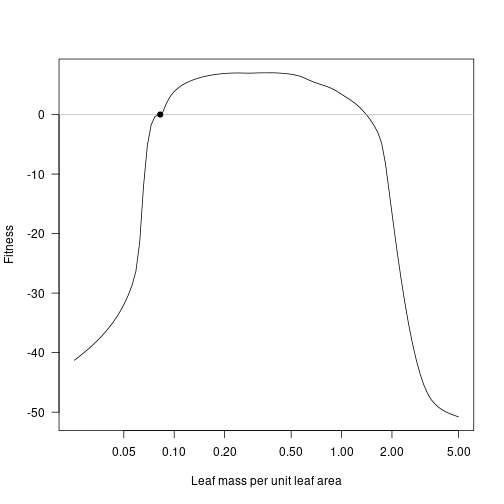
Zooming in in the vicinity of the result shows that this is disruptive selection: fitness increases to both sides of the resident!
lma_detail <- trait_matrix(seq_log(lma_attr * 0.95, lma_attr * 1.05, 51), "lma")
fitness_detail <- fitness_landscape(lma_detail, patch_eq_attr)
plot(lma_detail, fitness_detail, log="x", type="l", las=1,
xlab="Leaf mass per unit leaf area", ylab="Fitness")
abline(h=0, col="grey")
points(lma_attr, 0, pch=19)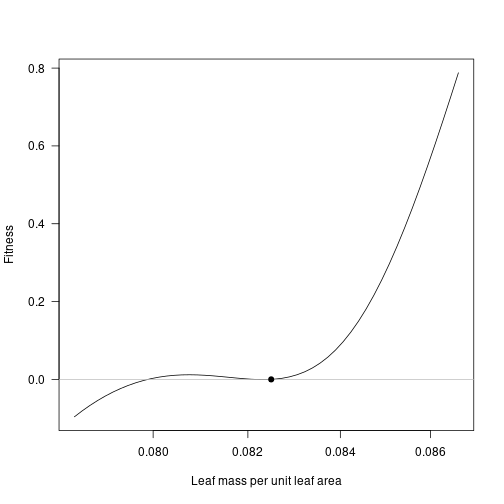
Invasion landscapes
Holding the first species at 0.0825 we can introduce additional species (it’s close enough to the optimum here, though in general this point might move substantially as new species are introduced).
Consider the point of maximum fitness:
lma_max <- lma[which.max(fitness_attr)]
lma_max## [1] 0.3748389
plot(lma, fitness_attr, log="x", type="l", las=1,
xlab="Leaf mass per unit leaf area", ylab="Fitness")
abline(h=0, col="grey")
points(lma_attr, 0, pch=19)
abline(v=lma_max, col="red")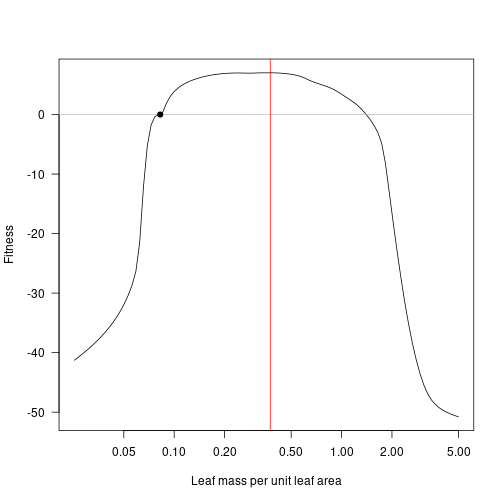
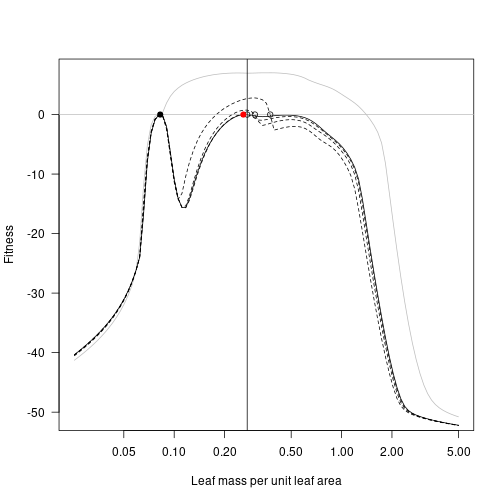
Introducing a new species the point of maximum fitness draws the fitness landscape down around the second species, with a fitness gradient that points towards increased LMA.
patch_eq_max <- add_eq(lma_max, patch_eq_attr)## [2021-02-25 12:32:25.755] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:32:25.755] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:32:34.520] schedule> 1: Splitting {0,21} times (213,141)
## [2021-02-25 12:32:34.520] schedule> 1: Splitting {0,21} times (213,141)
## [2021-02-25 12:32:43.749] equilibrium> eq> 1: {17.30636, 1} -> {12.22391, 17.26106} (delta = {-5.08245, 16.26106})
## [2021-02-25 12:32:43.749] equilibrium> eq> 1: {17.30636, 1} -> {12.22391, 17.26106} (delta = {-5.08245, 16.26106})
## [2021-02-25 12:32:52.296] schedule> 1: Splitting {15,14} times (141,141)
## [2021-02-25 12:32:52.296] schedule> 1: Splitting {15,14} times (141,141)
## [2021-02-25 12:33:02.664] schedule> 2: Splitting {2,4} times (156,155)
## [2021-02-25 12:33:02.664] schedule> 2: Splitting {2,4} times (156,155)
## [2021-02-25 12:33:13.237] equilibrium> eq> 2: {12.22391, 17.26106} -> {12.86662, 14.95559} (delta = {0.6427081, -2.305471})
## [2021-02-25 12:33:13.237] equilibrium> eq> 2: {12.22391, 17.26106} -> {12.86662, 14.95559} (delta = {0.6427081, -2.305471})
## [2021-02-25 12:33:23.467] equilibrium> eq> 3: {12.86662, 14.95559} -> {12.82323, 15.022} (delta = {-0.04338479, 0.06640538})
## [2021-02-25 12:33:23.467] equilibrium> eq> 3: {12.86662, 14.95559} -> {12.82323, 15.022} (delta = {-0.04338479, 0.06640538})
## [2021-02-25 12:33:33.954] equilibrium> eq> 4: {12.82323, 15.022} -> {12.82532, 15.02144} (delta = {0.002088111, -0.0005603039})
## [2021-02-25 12:33:33.954] equilibrium> eq> 4: {12.82323, 15.022} -> {12.82532, 15.02144} (delta = {0.002088111, -0.0005603039})
## [2021-02-25 12:33:33.955] equilibrium> Reached target accuracy (delta 2.08811e-03, 1.62838e-04 < 1.00000e-03 eps)
## [2021-02-25 12:33:33.955] equilibrium> Reached target accuracy (delta 2.08811e-03, 1.62838e-04 < 1.00000e-03 eps)
## [2021-02-25 12:33:33.955] equilibrium> Iteration 1 converged
## [2021-02-25 12:33:33.955] equilibrium> Iteration 1 converged
## [2021-02-25 12:33:33.955] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:33:33.955] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:33:46.043] schedule> 1: Splitting {0,14} times (213,141)
## [2021-02-25 12:33:46.043] schedule> 1: Splitting {0,14} times (213,141)
## [2021-02-25 12:33:57.421] schedule> 2: Splitting {0,4} times (213,155)
## [2021-02-25 12:33:57.421] schedule> 2: Splitting {0,4} times (213,155)
## [2021-02-25 12:34:09.462] equilibrium> eq> 1: {12.82323, 15.022} -> {12.83544, 15.02179} (delta = {0.01220595, -0.0002059787})
## [2021-02-25 12:34:09.462] equilibrium> eq> 1: {12.82323, 15.022} -> {12.83544, 15.02179} (delta = {0.01220595, -0.0002059787})
## [2021-02-25 12:34:09.462] equilibrium> Keeping species 1
## [2021-02-25 12:34:09.462] equilibrium> Keeping species 1
## [2021-02-25 12:34:21.498] equilibrium> eq> 2: {12.82323, 15.022} -> {12.83544, 15.02179} (delta = {0.01220593, -0.0002059979})
## [2021-02-25 12:34:21.498] equilibrium> eq> 2: {12.82323, 15.022} -> {12.83544, 15.02179} (delta = {0.01220593, -0.0002059979})
## [2021-02-25 12:34:33.541] equilibrium> eq> 3: {12.82323, 15.022} -> {12.83544, 15.02179} (delta = {0.01220593, -0.0002059979})
## [2021-02-25 12:34:33.541] equilibrium> eq> 3: {12.82323, 15.022} -> {12.83544, 15.02179} (delta = {0.01220593, -0.0002059979})
## [2021-02-25 12:34:33.542] equilibrium> Solve 1 converged
## [2021-02-25 12:34:33.542] equilibrium> Solve 1 converged
## [2021-02-25 12:34:33.542] equilibrium> Accepting solution via solver
## [2021-02-25 12:34:33.542] equilibrium> Accepting solution via solver
fitness_max <- fitness_landscape(lma, patch_eq_max)
plot(lma, fitness_attr, log="x", type="l", las=1,
xlab="Leaf mass per unit leaf area", ylab="Fitness", col="grey")
lines(lma, fitness_max)
abline(h=0, col="grey")
points(lma_attr, 0, pch=19)
points(lma_max, 0, pch=19, col="red")
lma_max_2 <- lma[which.max(fitness_max)]
abline(v=lma_max_2)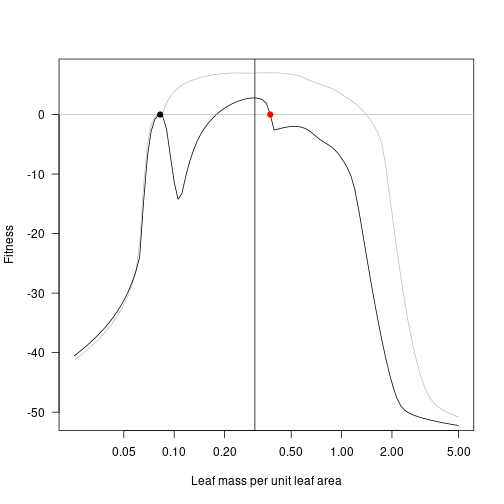
At the cost of extremely tedious copy/paste code, here is the result of repeatedly taking the lma value with highest fitness and moving the second species to this point, running to equilibrium, and plotting. For comparison the previous landscapes are retained as dotted lines.
patch_eq_max_2 <- add_eq(lma_max_2, patch_eq_attr)## [2021-02-25 12:40:48.937] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:40:48.937] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:40:58.025] schedule> 1: Splitting {0,23} times (213,141)
## [2021-02-25 12:40:58.025] schedule> 1: Splitting {0,23} times (213,141)
## [2021-02-25 12:41:07.483] equilibrium> eq> 1: {17.30636, 1} -> {12.01292, 17.08176} (delta = {-5.293438, 16.08176})
## [2021-02-25 12:41:07.483] equilibrium> eq> 1: {17.30636, 1} -> {12.01292, 17.08176} (delta = {-5.293438, 16.08176})
## [2021-02-25 12:41:15.117] schedule> 1: Splitting {15,17} times (141,141)
## [2021-02-25 12:41:15.117] schedule> 1: Splitting {15,17} times (141,141)
## [2021-02-25 12:41:23.755] schedule> 2: Splitting {3,2} times (156,158)
## [2021-02-25 12:41:23.755] schedule> 2: Splitting {3,2} times (156,158)
## [2021-02-25 12:41:32.830] equilibrium> eq> 2: {12.01292, 17.08176} -> {12.36448, 15.79908} (delta = {0.3515555, -1.282681})
## [2021-02-25 12:41:32.830] equilibrium> eq> 2: {12.01292, 17.08176} -> {12.36448, 15.79908} (delta = {0.3515555, -1.282681})
## [2021-02-25 12:41:42.435] equilibrium> eq> 3: {12.36448, 15.79908} -> {12.34319, 15.84398} (delta = {-0.02128601, 0.0448966})
## [2021-02-25 12:41:42.435] equilibrium> eq> 3: {12.36448, 15.79908} -> {12.34319, 15.84398} (delta = {-0.02128601, 0.0448966})
## [2021-02-25 12:41:52.109] equilibrium> eq> 4: {12.34319, 15.84398} -> {12.34414, 15.84312} (delta = {0.0009458628, -0.0008565372})
## [2021-02-25 12:41:52.109] equilibrium> eq> 4: {12.34319, 15.84398} -> {12.34414, 15.84312} (delta = {0.0009458628, -0.0008565372})
## [2021-02-25 12:41:52.110] equilibrium> Reached target accuracy (delta 9.45863e-04, 7.66303e-05 < 1.00000e-03 eps)
## [2021-02-25 12:41:52.110] equilibrium> Reached target accuracy (delta 9.45863e-04, 7.66303e-05 < 1.00000e-03 eps)
## [2021-02-25 12:41:52.110] equilibrium> Iteration 1 converged
## [2021-02-25 12:41:52.110] equilibrium> Iteration 1 converged
## [2021-02-25 12:41:52.111] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:41:52.111] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:42:03.437] schedule> 1: Splitting {1,17} times (213,141)
## [2021-02-25 12:42:03.437] schedule> 1: Splitting {1,17} times (213,141)
## [2021-02-25 12:42:14.530] schedule> 2: Splitting {0,2} times (214,158)
## [2021-02-25 12:42:14.530] schedule> 2: Splitting {0,2} times (214,158)
## [2021-02-25 12:42:25.702] equilibrium> eq> 1: {12.34319, 15.84398} -> {12.35551, 15.85483} (delta = {0.01231563, 0.01084816})
## [2021-02-25 12:42:25.702] equilibrium> eq> 1: {12.34319, 15.84398} -> {12.35551, 15.85483} (delta = {0.01231563, 0.01084816})
## [2021-02-25 12:42:25.703] equilibrium> Keeping species 1, 2
## [2021-02-25 12:42:25.703] equilibrium> Keeping species 1, 2
## [2021-02-25 12:42:36.877] equilibrium> eq> 2: {12.34319, 15.84398} -> {12.35551, 15.85483} (delta = {0.01231563, 0.01084813})
## [2021-02-25 12:42:36.877] equilibrium> eq> 2: {12.34319, 15.84398} -> {12.35551, 15.85483} (delta = {0.01231563, 0.01084813})
## [2021-02-25 12:42:47.979] equilibrium> eq> 3: {12.34319, 15.84398} -> {12.35551, 15.85483} (delta = {0.01231563, 0.01084813})
## [2021-02-25 12:42:47.979] equilibrium> eq> 3: {12.34319, 15.84398} -> {12.35551, 15.85483} (delta = {0.01231563, 0.01084813})
## [2021-02-25 12:42:47.980] equilibrium> Solve 1 converged
## [2021-02-25 12:42:47.980] equilibrium> Solve 1 converged
## [2021-02-25 12:42:47.980] equilibrium> Accepting solution via solver
## [2021-02-25 12:42:47.980] equilibrium> Accepting solution via solver
fitness_max_2 <- fitness_landscape(lma, patch_eq_max_2)
plot(lma, fitness_attr, log="x", type="l", las=1,
xlab="Leaf mass per unit leaf area", ylab="Fitness", col="grey")
lines(lma, fitness_max, lty=2)
lines(lma, fitness_max_2)
abline(h=0, col="grey")
points(lma_attr, 0, pch=19)
points(lma_max, 0)
points(lma_max_2, 0, pch=19, col="red")
lma_max_3 <- lma[which.max(fitness_max_2)]
abline(v=lma_max_3)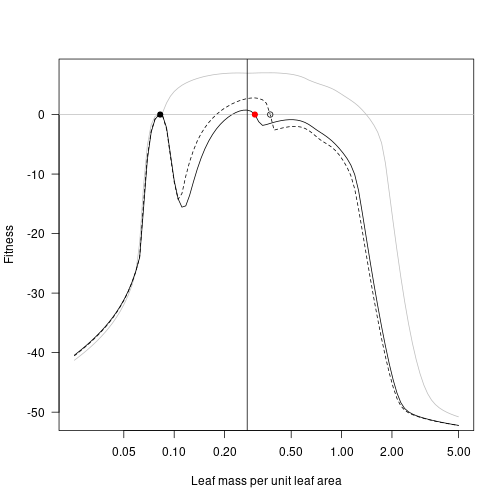
patch_eq_max_3 <- add_eq(lma_max_3, patch_eq_attr)## [2021-02-25 12:48:42.903] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:48:42.903] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:48:52.594] schedule> 1: Splitting {0,20} times (213,141)
## [2021-02-25 12:48:52.594] schedule> 1: Splitting {0,20} times (213,141)
## [2021-02-25 12:49:02.534] schedule> 2: Splitting {0,2} times (213,161)
## [2021-02-25 12:49:02.534] schedule> 2: Splitting {0,2} times (213,161)
## [2021-02-25 12:49:12.230] equilibrium> eq> 1: {17.30636, 1} -> {12.01147, 16.52161} (delta = {-5.294885, 15.52161})
## [2021-02-25 12:49:12.230] equilibrium> eq> 1: {17.30636, 1} -> {12.01147, 16.52161} (delta = {-5.294885, 15.52161})
## [2021-02-25 12:49:19.969] schedule> 1: Splitting {15,21} times (141,141)
## [2021-02-25 12:49:19.969] schedule> 1: Splitting {15,21} times (141,141)
## [2021-02-25 12:49:29.683] schedule> 2: Splitting {4,1} times (156,162)
## [2021-02-25 12:49:29.683] schedule> 2: Splitting {4,1} times (156,162)
## [2021-02-25 12:49:39.441] equilibrium> eq> 2: {12.01147, 16.52161} -> {12.08184, 16.30608} (delta = {0.07036873, -0.215529})
## [2021-02-25 12:49:39.441] equilibrium> eq> 2: {12.01147, 16.52161} -> {12.08184, 16.30608} (delta = {0.07036873, -0.215529})
## [2021-02-25 12:49:49.344] equilibrium> eq> 3: {12.08184, 16.30608} -> {12.08062, 16.30764} (delta = {-0.001220601, 0.00156395})
## [2021-02-25 12:49:49.344] equilibrium> eq> 3: {12.08184, 16.30608} -> {12.08062, 16.30764} (delta = {-0.001220601, 0.00156395})
## [2021-02-25 12:49:49.345] equilibrium> Reached target accuracy (delta 1.56395e-03, 1.01028e-04 < 1.00000e-03 eps)
## [2021-02-25 12:49:49.345] equilibrium> Reached target accuracy (delta 1.56395e-03, 1.01028e-04 < 1.00000e-03 eps)
## [2021-02-25 12:49:49.345] equilibrium> Iteration 1 converged
## [2021-02-25 12:49:49.345] equilibrium> Iteration 1 converged
## [2021-02-25 12:49:49.346] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:49:49.346] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:50:01.017] schedule> 1: Splitting {0,19} times (213,141)
## [2021-02-25 12:50:01.017] schedule> 1: Splitting {0,19} times (213,141)
## [2021-02-25 12:50:12.328] schedule> 2: Splitting {0,1} times (213,160)
## [2021-02-25 12:50:12.328] schedule> 2: Splitting {0,1} times (213,160)
## [2021-02-25 12:50:23.827] equilibrium> eq> 1: {12.08184, 16.30608} -> {12.09272, 16.3084} (delta = {0.01087391, 0.002320391})
## [2021-02-25 12:50:23.827] equilibrium> eq> 1: {12.08184, 16.30608} -> {12.09272, 16.3084} (delta = {0.01087391, 0.002320391})
## [2021-02-25 12:50:23.828] equilibrium> Keeping species 1, 2
## [2021-02-25 12:50:23.828] equilibrium> Keeping species 1, 2
## [2021-02-25 12:50:35.349] equilibrium> eq> 2: {12.08184, 16.30608} -> {12.09272, 16.3084} (delta = {0.0108739, 0.002320425})
## [2021-02-25 12:50:35.349] equilibrium> eq> 2: {12.08184, 16.30608} -> {12.09272, 16.3084} (delta = {0.0108739, 0.002320425})
## [2021-02-25 12:50:46.903] equilibrium> eq> 3: {12.08184, 16.30608} -> {12.09272, 16.3084} (delta = {0.0108739, 0.002320425})
## [2021-02-25 12:50:46.903] equilibrium> eq> 3: {12.08184, 16.30608} -> {12.09272, 16.3084} (delta = {0.0108739, 0.002320425})
## [2021-02-25 12:50:46.904] equilibrium> Solve 1 converged
## [2021-02-25 12:50:46.904] equilibrium> Solve 1 converged
## [2021-02-25 12:50:46.904] equilibrium> Accepting solution via solver
## [2021-02-25 12:50:46.904] equilibrium> Accepting solution via solver
fitness_max_3 <- fitness_landscape(lma, patch_eq_max_3)
plot(lma, fitness_attr, log="x", type="l", las=1,
xlab="Leaf mass per unit leaf area", ylab="Fitness", col="grey")
lines(lma, fitness_max, lty=2)
lines(lma, fitness_max_2, lty=2)
lines(lma, fitness_max_3)
abline(h=0, col="grey")
points(lma_attr, 0, pch=19)
points(lma_max, 0)
points(lma_max_2, 0)
points(lma_max_3, 0, pch=19, col="red")
lma_max_4 <- lma[which.max(fitness_max_3)]
abline(v=lma_max_4)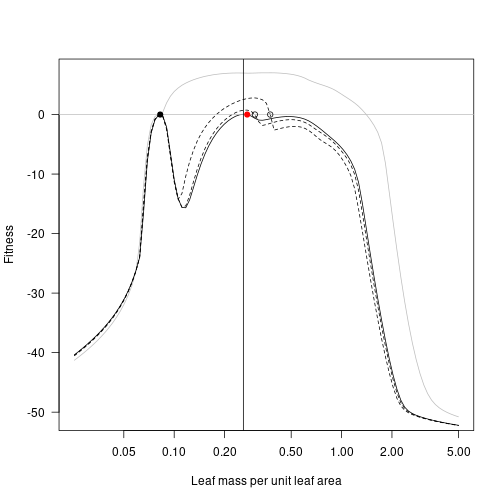
patch_eq_max_4 <- add_eq(lma_max_4, patch_eq_attr)## [2021-02-25 12:56:55.515] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:56:55.515] equilibrium> Solving seed rain using hybrid
## [2021-02-25 12:57:04.967] schedule> 1: Splitting {0,22} times (213,141)
## [2021-02-25 12:57:04.967] schedule> 1: Splitting {0,22} times (213,141)
## [2021-02-25 12:57:14.460] schedule> 2: Splitting {0,4} times (213,163)
## [2021-02-25 12:57:14.460] schedule> 2: Splitting {0,4} times (213,163)
## [2021-02-25 12:57:24.430] equilibrium> eq> 1: {17.30636, 1} -> {12.03605, 16.1373} (delta = {-5.27031, 15.1373})
## [2021-02-25 12:57:24.430] equilibrium> eq> 1: {17.30636, 1} -> {12.03605, 16.1373} (delta = {-5.27031, 15.1373})
## [2021-02-25 12:57:32.149] schedule> 1: Splitting {16,21} times (141,141)
## [2021-02-25 12:57:32.149] schedule> 1: Splitting {16,21} times (141,141)
## [2021-02-25 12:57:42.126] schedule> 2: Splitting {4,1} times (157,162)
## [2021-02-25 12:57:42.126] schedule> 2: Splitting {4,1} times (157,162)
## [2021-02-25 12:57:51.926] equilibrium> eq> 2: {12.03605, 16.1373} -> {11.96548, 16.56598} (delta = {-0.07057156, 0.4286856})
## [2021-02-25 12:57:51.926] equilibrium> eq> 2: {12.03605, 16.1373} -> {11.96548, 16.56598} (delta = {-0.07057156, 0.4286856})
## [2021-02-25 12:58:01.602] equilibrium> eq> 3: {11.96548, 16.56598} -> {11.96313, 16.57663} (delta = {-0.002351885, 0.01064882})
## [2021-02-25 12:58:01.602] equilibrium> eq> 3: {11.96548, 16.56598} -> {11.96313, 16.57663} (delta = {-0.002351885, 0.01064882})
## [2021-02-25 12:58:01.602] equilibrium> Reached target accuracy (delta 1.06488e-02, 6.42812e-04 < 1.00000e-03 eps)
## [2021-02-25 12:58:01.602] equilibrium> Reached target accuracy (delta 1.06488e-02, 6.42812e-04 < 1.00000e-03 eps)
## [2021-02-25 12:58:01.603] equilibrium> Iteration 1 converged
## [2021-02-25 12:58:01.603] equilibrium> Iteration 1 converged
## [2021-02-25 12:58:01.603] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:58:01.603] equilibrium> Solving seed rain using nleqslv
## [2021-02-25 12:58:12.815] schedule> 1: Splitting {0,21} times (213,141)
## [2021-02-25 12:58:12.815] schedule> 1: Splitting {0,21} times (213,141)
## [2021-02-25 12:58:24.253] schedule> 2: Splitting {0,1} times (213,162)
## [2021-02-25 12:58:24.253] schedule> 2: Splitting {0,1} times (213,162)
## [2021-02-25 12:58:35.709] equilibrium> eq> 1: {11.96548, 16.56598} -> {11.97546, 16.57718} (delta = {0.009985282, 0.01119273})
## [2021-02-25 12:58:35.709] equilibrium> eq> 1: {11.96548, 16.56598} -> {11.97546, 16.57718} (delta = {0.009985282, 0.01119273})
## [2021-02-25 12:58:35.709] equilibrium> Keeping species 1, 2
## [2021-02-25 12:58:35.709] equilibrium> Keeping species 1, 2
## [2021-02-25 12:58:47.172] equilibrium> eq> 2: {11.96548, 16.56598} -> {11.97546, 16.57718} (delta = {0.009985294, 0.01119281})
## [2021-02-25 12:58:47.172] equilibrium> eq> 2: {11.96548, 16.56598} -> {11.97546, 16.57718} (delta = {0.009985294, 0.01119281})
## [2021-02-25 12:58:58.640] equilibrium> eq> 3: {11.96548, 16.56598} -> {11.97546, 16.57718} (delta = {0.009985294, 0.01119281})
## [2021-02-25 12:58:58.640] equilibrium> eq> 3: {11.96548, 16.56598} -> {11.97546, 16.57718} (delta = {0.009985294, 0.01119281})
## [2021-02-25 12:58:58.640] equilibrium> Solve 1 converged
## [2021-02-25 12:58:58.640] equilibrium> Solve 1 converged
## [2021-02-25 12:58:58.641] equilibrium> Accepting solution via solver
## [2021-02-25 12:58:58.641] equilibrium> Accepting solution via solver
fitness_max_4 <- fitness_landscape(lma, patch_eq_max_4)
plot(lma, fitness_attr, log="x", type="l", las=1,
xlab="Leaf mass per unit leaf area", ylab="Fitness", col="grey")
lines(lma, fitness_max, lty=2)
lines(lma, fitness_max_2, lty=2)
lines(lma, fitness_max_3, lty=2)
lines(lma, fitness_max_4)
abline(h=0, col="grey")
points(lma_attr, 0, pch=19)
points(lma_max, 0)
points(lma_max_2, 0)
points(lma_max_3, 0)
points(lma_max_4, 0, pch=19, col="red")
lma_max_5 <- lma[which.max(fitness_max_4)]
abline(v=lma_max_5)