(Standardized) major axis estimation and testing for one or several samples

Source: R/sma.R

The sma and ma functions fit SMA and MA respectively, and construct confidence intervals or test hypotheses about slope or elevation in one or several samples, depending on how the arguments are specified. Options exist to force lines through the origin, (approximately) correct for measurement error if the measurement error variance is known, and use robust estimation to ensure that inferences are valid in the presence of outliers (currently implemented for single samples only).

sma(
  formula,
  data,
  subset,
  na.action,
  log = "",
  method = c("SMA", "MA", "OLS"),
  type = c("elevation", "shift"),
  alpha = 0.05,
  slope.test = NA,
  elev.test = NA,
  multcomp = FALSE,
  multcompmethod = c("default", "adjusted"),
  robust = FALSE,
  V = matrix(0, 2, 2),
  n_min = 3,
  quiet = FALSE,
  ...
)

Arguments

formula

Formula of the form y ~ x etc. This determines whether a single (S)MA is fitted, or whether several lines are fitted and compared. See Details.

data

A dataframe with the x and y variables.

subset

A subset of the dataframe for fitting; optional.

na.action

What to do with missing values (na.omit, na.fail, etc).

log

One of 'x', 'y', or 'xy' to log10-transform variables.

method

If SMA, standardized major axis, if MA, major axis, and if OLS, ordinary least squares.

type

If several lines with common slope are to be compared, do you want to test for a change in 'elevation' or for a 'shift' along a common (S)MA. See Details.

alpha

The error rate for confidence intervals. Typically 0.05.

slope.test

The hypothesised value to be used, if testing for evidence that (S)MA slope(s) are significantly different from a hypothesised value.

elev.test

The hypothesised value to be used, if testing for evidence that (S)MA elevation(s) are significantly different from a hypothesised value.

multcomp

Logical. If TRUE, performs pair-wise comparisons between levels of the grouping variable.

multcompmethod

Whether to adjust the P values for multiple comparisons ('adjusted') or not ('default').

robust

If TRUE, uses a new method of robust line fitting. (Currently available for single-sample testing only.)

V

The estimated variance matrix of measurement error. Average measurement error for Y is in the first row and column, and average measurement error for X is in the second row and column. The default is that there is no measurement error.

n_min

The minimum sample size for a group.

quiet

If TRUE, suppresses all messages.

...

Further arguments passed to internal functions (none at the moment?)

Value

An object of class sma or ma, which contains the following output arguments:

coef

The coefficients of the fitted (standardised) major axes. If several samples are being compared, this will return parameters from the alternative model, e.g. assuming separate slopes if testing for common slope, or assuming common slope but separate elevations if testing for common elevation.

nullcoef

The coefficients under the null hypothesis

alpha

As above.

method

The method used in fitting lines: 'MA' or 'SMA'

intercept

Whether or not (S)MA lines were forced through the origin (True or False).

call

The call to the ma or sma function.

data

As above.

log

As above.

variables

A list of the variables used in fitting (S)MA lines.

origvariables

A list of the variables prior to transformation (if any) for use in fitting (S)MA lines.

groups

Levels of the grouping variable, if present in the fit.

gt

Type of grouptest ("slopecom","elevcom",or "shiftcom"), if it was carried out, or "none" if none.

gtr

The result of that grouptest.

slopetest

Output from the hypothesis test of slope(s), if any. Returned as a list of objects, including the P-value (p), the test statistic (r or LR), the (common) slope (b) and its confidence interval (ci).

elevtest

Output from the hypothesis test of elevation(s), if any. Returned as a list of objects, including the P-value (p), the test statistic (t or stat), the (common) elevation (a) and its confidence interval (ci).

slopetestdone

Whether a slopetest was actually carried out.

elevtestdone

Whether an elevation test was actually carried out.

n

Sample size(s).

r2

Squared correlation coefficient.

pval

P-value of the test of correlation coefficient against zero.

from,to

X values corresponding the maximum and minimum fitted values in each group. Used by plot.sma to determine endpoints for fitted lines).

groupsummary

Neatly organized dataframe with coefficients by group.

Details

This is the key function in the smatr-package; all the key estimation and testing functionality in the package can all be accessed using this function, via different usages of the formula and other arguments, as described below.

One-sample testing The below options allow estimation of a (S)MA, confidence intervals for parameters, and hypothesis testing of parameters, from a single sample of two variables y and x. Use the sma function to fit a standardised major axis (SMA), or use ma in combination with the below options in order to fit major axis (MA) instead.

list("sma(y~x)")

Fits a SMA and constructs confidence intervals for the true slope and elevation. Replaces the line.cis function from previous versions of smatr.

list("ma(y~x)")

Fits a MA and constructs confidence intervals for the true slope and elevation. All the below functions also work for MA, if the ma function is called instead of the sma function.

list("sma(y~x, slope.test=B)")

Tests if the slope of a SMA equals B.

list("sma(y~x, elev.test=A)")

Tests if the elevation of a SMA equals A.

list("sma(y~x, robust=T)")

Fits a SMA using Huber's M estimation and constructs confidence intervals for the true slope and elevation. This offers robustness to outliers in estimation and inference, and can be used in combination with the slope.test and elev.test arguments.

list("sma(y~x-1)")

Fits a SMA where the line is forced through the origin, and constructs confidence intervals for the true slope. This type of formula can be used in combination with the slope.test argument.

For several samples: The below options allow estimation of several (S)MA lines, confidence intervals for parameters, and hypothesis testing of parameters, from two variables y and x for observations that have been classified into several different samples using the factor groups. Use the sma function to fit a standardised major axis (SMA), or use the ma in combination with the below options in order to fir major axis (MA) instead.

list("sma(y~x*groups)")

Test if several SMA lines share a common slope, and construct a confidence interval for the true common slope.

list("sma(y~x+groups, type="elevation")")

Test if several common slope SMA lines also share a common elevation, and construct a confidence interval for the true common elevation.

list("sma(y~x+groups, type="shift")")

Test if several groups of observations have no shift in location along common slope SMA lines.

list("sma(y~x*groups, slope.test=B)")

Test if several SMA lines share a common slope whose true value is exactly equal to B.

list("sma(y~x+groups, elev.test=A)")

Test if several common-slope SMA lines share a common elevation whose true value is exactly equal to A.

list("sma(y~x*groups-1)")

Test if several SMA lines forced through the origin share a common slope. This can also be used in combination with the slope.test argument or when testing for no shift along common (S)MA lines.

In all cases, estimates and confidence intervals for key parameters are returned, and if a hypothesis test is done, results will be returned and stored in the slope.test or elev.test output arguments.

The plot function can be applied to objects produced using the sma and ma functions, which is highly recommended to visualise results and check assumptions.

Multiple comparisons If multcomp=TRUE, pair-wise comparisons are made between levels of the grouping variable for differences in slope, elevation or shift, depending on the formula used. The P values can be adjusted for multiple comparisons (using the Sidak correction). See also multcompmatrix for visualization of the results. Warning: When using the multiple comparisons (multcomp=TRUE), you must specify a data statement. If your variables are not in a dataframe, simply combine them in a dataframe before calling sma.

References

Warton, D.I., R.A. Duursma, D.S. Falster and S. Taskinen (2012). smatr 3 - an R package for estimation and inference about allometric lines. Methods in Ecology and Evolution. 3, 257-259.

Warton D. I. and Weber N. C. (2002) Common slope tests for bivariate structural relationships. Biometrical Journal 44, 161--174.

Warton D. I., Wright I. J., Falster D. S. and Westoby M. (2006) A review of bivariate line-fitting methods for allometry. Biological Reviews 81, 259--291.

Taskinen S. and Warton D. I. (in press) Robust estimation and inference for bivariate line-fitting in allometry. Biometrical Journal.

See also

plot.sma

Author

Warton, D. I. David.Warton@unsw.edu.au, R.A. Duursma, D. Falster, S. Taskinen

Examples



# Load leaf lifetime dataset:
data(leaflife)

### One sample analyses ###
# Extract only low-nutrient, low-rainfall data:
leaf.low <- subset(leaflife, soilp == 'low' & rain == 'low')

# Fit a MA for log(leaf longevity) vs log(leaf mass per area):
ma(longev ~ lma, log='xy', data=leaflife)
#> Call: sma(formula = ..1, data = ..3, log = "xy", method = "MA") 
#> 
#> Fit using Major Axis 
#> 
#> These variables were log-transformed before fitting: xy 
#> 
#> Confidence intervals (CI) are at 95%
#> 
#> ------------------------------------------------------------
#> Coefficients:
#>             elevation    slope
#> estimate    -3.085214 1.492616
#> lower limit -3.968020 1.146777
#> upper limit -2.202407 2.001084
#> 
#> H0 : variables uncorrelated
#> R-squared : 0.4544809 
#> P-value : 4.0171e-10 
#> 

# Test if the MA slope is not significantly different from 1:
ma.test <- ma(longev ~ lma, log='xy', slope.test=1, data=leaflife)
summary(ma.test)
#>       group  n        r2        pval    Slope Slope_lowCI Slope_highCI
#> group   all 67 0.4544809 4.01707e-10 1.492616    1.146777     2.001084
#>             Int Int_lowCI Int_highCI Slope_test Slope_test_p Elev_test
#> group -3.085214  -3.96802  -2.202407          1  0.003539277        NA
#>       Elev_test_p
#> group          NA

# Construct a residual plot to check assumptions:
plot(ma.test,type="residual")


### Several sample analyses ###

# Now consider low-nutrient sites (high and low rainfall):
leaf.low.soilp <- subset(leaflife, soilp == 'low')

# Fit SMA's separately at each of high and low rainfall sites,
# and test for common slope:
com.test <- sma(longev~lma*rain, log="xy", data=leaf.low.soilp)
com.test
#> Call: sma(formula = longev ~ lma * rain, data = leaf.low.soilp, log = "xy") 
#> 
#> Fit using Standardized Major Axis 
#> 
#> These variables were log-transformed before fitting: xy 
#> 
#> Confidence intervals (CI) are at 95%
#> 
#> ------------------------------------------------------------
#> Results of comparing lines among groups.
#> 
#> H0 : slopes are equal.
#> Likelihood ratio statistic : 2.367 with 1 degrees of freedom
#> P-value : 0.12395 
#> ------------------------------------------------------------
#> 
#> Use the summary() function to print coefficients by group.

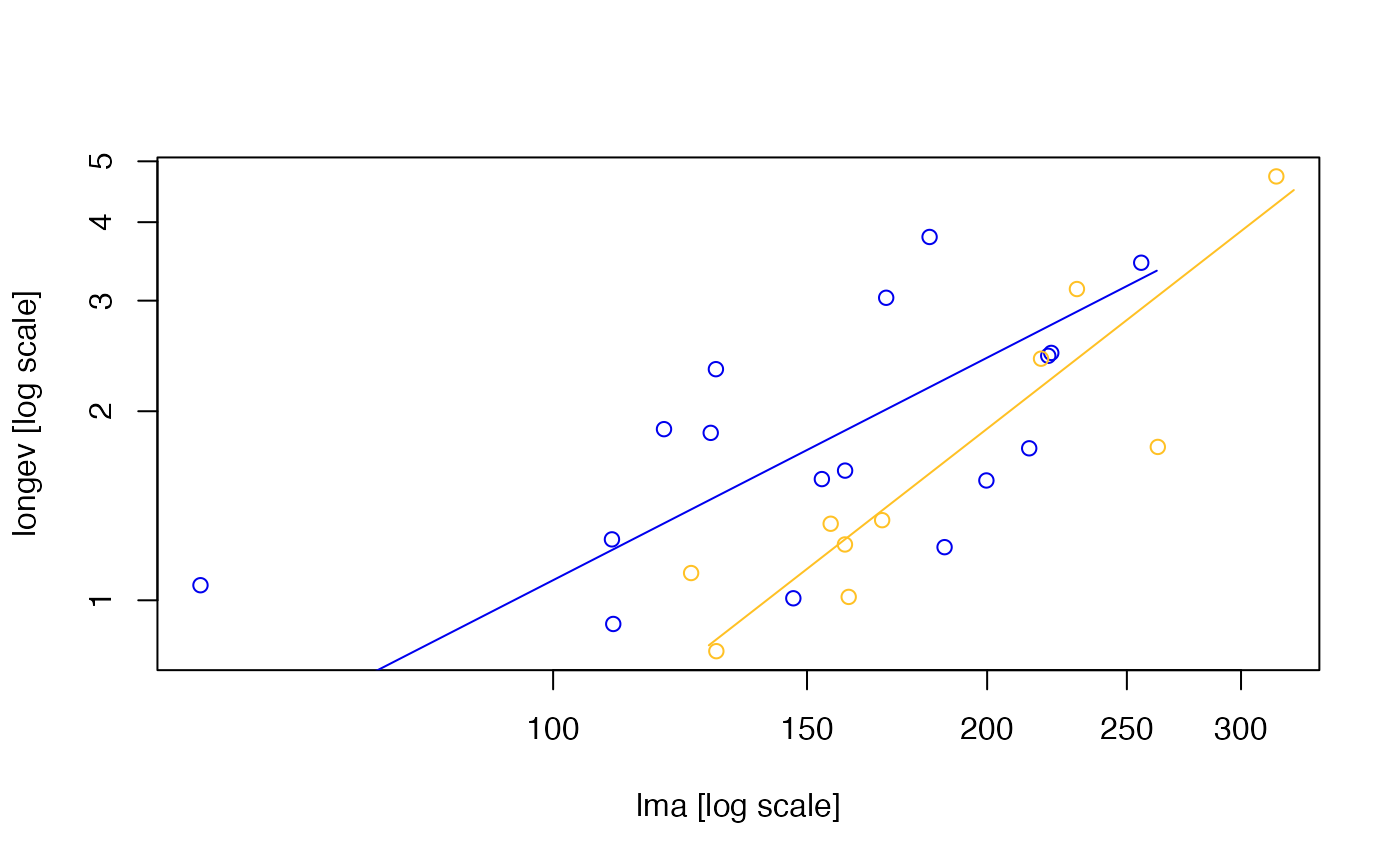
# Plot longevity vs LMA separately for each group:
plot(com.test)


# Fit SMA's separately at each of high and low rainfall sites,
# and test if there is a common slope equal to 1:
sma(longev~lma*rain, log="xy", slope.test=1, data=leaf.low.soilp)
#> Call: sma(formula = longev ~ lma * rain, data = leaf.low.soilp, log = "xy", 
#>     slope.test = 1) 
#> 
#> Fit using Standardized Major Axis 
#> 
#> These variables were log-transformed before fitting: xy 
#> 
#> Confidence intervals (CI) are at 95%
#> 
#> ------------------------------------------------------------
#> Results of comparing lines among groups.
#> 
#> H0 : slopes are equal.
#> Likelihood ratio statistic : 2.367 with 1 degrees of freedom
#> P-value : 0.12395 
#> ------------------------------------------------------------
#> 
#> H0 : common slope not different from 1 
#> Likelihood ratio statistic = 8.677 with 2 degrees of freedom under H0
#> P-value : 0.013057 
#> 
#> Use the summary() function to print coefficients by group.

# Fit SMA's with common slope across each of high and low rainfall sites, 
# and test for common elevation:
sma(longev~lma+rain, log="xy", data=leaf.low.soilp)
#> Call: sma(formula = longev ~ lma + rain, data = leaf.low.soilp, log = "xy") 
#> 
#> Fit using Standardized Major Axis 
#> 
#> These variables were log-transformed before fitting: xy 
#> 
#> Confidence intervals (CI) are at 95%
#> 
#> ------------------------------------------------------------
#> Results of comparing lines among groups.
#> 
#> H0 : slopes are equal.
#> Likelihood ratio statistic : 2.367 with 1 degrees of freedom
#> P-value : 0.12395 
#> ------------------------------------------------------------
#> 
#> H0 : no difference in elevation.
#> Wald statistic: 6.566 with 1 degrees of freedom
#> P-value : 0.010393 
#> ------------------------------------------------------------
#> 
#> Use the summary() function to print coefficients by group.

# Fit SMA's with common slope across each of high and low rainfall sites, 
# and test for no shift along common SMA:
sma(longev~lma+rain, log="xy", type="shift", data=leaf.low.soilp)
#> Call: sma(formula = longev ~ lma + rain, data = leaf.low.soilp, log = "xy", 
#>     type = "shift") 
#> 
#> Fit using Standardized Major Axis 
#> 
#> These variables were log-transformed before fitting: xy 
#> 
#> Confidence intervals (CI) are at 95%
#> 
#> ------------------------------------------------------------
#> Results of comparing lines among groups.
#> 
#> H0 : slopes are equal.
#> Likelihood ratio statistic : 2.367 with 1 degrees of freedom
#> P-value : 0.12395 
#> ------------------------------------------------------------
#> 
#> H0 : no shift along common axis.
#> Wald statistic: 0.2091 with 1 degrees of freedom
#> P-value : 0.64745 
#> ------------------------------------------------------------
#> 
#> Use the summary() function to print coefficients by group.